If we want to move towards a world where models are “always training” and continually learning from experience over time, we need to address a basic challenge: how do we keep updating the parameters of a model without breaking it? In this post, I’ll motivate memory layers as a natural architecture for this paradigm: high-capacity, but sparse (few active parameters) on each forward pass. In our recent paper, we found that finetuning memory layers enables learning without forgetting much more effectively than LoRA: when learning TriviaQA facts, NaturalQuestions performance drops by 89% with full finetuning and 71% with LoRA, but only 11% with memory layers. Along the way, I’ll also discuss the challenges of the continual learning problem broadly.

Check out the paper here: Continual Learning via Sparse Memory Finetuning

Generalization vs. Integration

Continual learning has been studied for decades at this point. I think a lot of the discussion today is muddied by the fact that there are many classic formalizations of this idea, potentially none of which align with what we think of as real-world continual learning.

Intuitively, what many people think of is a system that can be taught like an intern: every time it encounters a new experience, learns a new fact, or gets feedback from the user, the system should get smarter over time, just like people do.

What are the research questions we need to solve before this is a reality?

I think of continual learning as two subproblems:

Generalization: given a piece of data (user feedback, a piece of experience, etc.), what update should we do to learn the “important bits” from that data?

Learning to regurgitate information is easy (just overfit / memorize). The challenge is learning something that can be used in diverse future settings. This is well-understood now for fact learning: when we see a string like “Barack Obama was born in Hawaii” in the training corpus, what I want the model to learn is not that the word Hawaii always follows in, but the semantic content that the tokens represent: “Barack Obama,” a real-world entity, was “born” (abstractly, “came into existence”) in “Hawaii,” a real-world entity. From the perspective of a language model consuming the raw tokens, it’s ambiguous which “hypothesis” it’s trying to learn from the data. This explains why paraphrasing is necessary to robustly teach models new facts (Physics of Language Models). Augmentation disambiguates what hypothesis we want the model to learn.

This is less clear for other types of data. If the model is learning from a math textbook, what augmentations would help? Or if an agent tries a coding problem and fails to solve it, what update should we apply? This is the essence of effective human learning: a good math student doesn’t read a textbook in one pass, but comes up with their own augmentations: working through some toy examples, combining the theorems with ones they already know, etc. This was the intuition behind our recent paper: language models learn much more effectively with Active Reading. We found general augmentations beyond paraphrasing even help dramatically with factual retention, but it’s yet to be seen how well this works for other data.

Better generalization comes down to the fact that we implicitly expect continually learning systems to self-supervise in more sophisticated ways, since most of the world doesn’t provide a neatly packaged SFT dataset or environment to RL on. Naive next-token prediction on the raw data stream isn’t enough. There’s a lot more to say here, but in our work we tackle the second challenge: forgetting and integration.

Forgetting/Integration: given a piece of data, how do we integrate it with what we already know?

The other side of the coin is not forgetting what we’ve already learned: the classic catastrophic forgetting problem. I think integration is a more accurate term for the behavior we want – sometimes we do want to “forget” or update things we knew previously, like the fact that the current president of the United States is no longer Obama.

A system that only adds to its knowledge (e.g. by adding new MoE experts for new tasks) never forgets, but doesn’t compress information in the right way. Is the expected behavior with the query “Who is the current president of the United States” for the model to upweight new expert N+1 over expert 1,…,N? Having conflicting knowledge in the model seems like it would only worsen robustness issues, and additionally doesn’t fully allow the model to benefit from transfer between tasks across its lifetime the same way pretraining does. To solve catastrophic forgetting and integration, we’ll likely want solutions where models can learn what to overwrite and what to preserve, without artificial boundaries between “new” and “old” knowledge. In our paper, “Continual Learning via Sparse Memory Finetuning,” we propose that memory layers provide a potential answer.

The Design Space

To motivate memory layers, let’s consider the design space of solutions. Intuitively, we don’t want to update all the parameters of a model when learning a new piece of information, and work like grafting has shown that we don’t need to: the set of parameters responsible for a particular task is often a very sparse set (~0.01%).

What we want is a system with:

• Targeted updates: touches only the minimal set of parameters needed to learn a particular data point
• High capacity: scales to large amounts of new information for lifelong learning
• Adaptive integration: learns how to partition and organize information based on the input—overwriting when needed, transferring skills between tasks when helpful, etc.

With this in mind, let’s consider commonly proposed solutions to lifelong learning or personalization for LLMs:

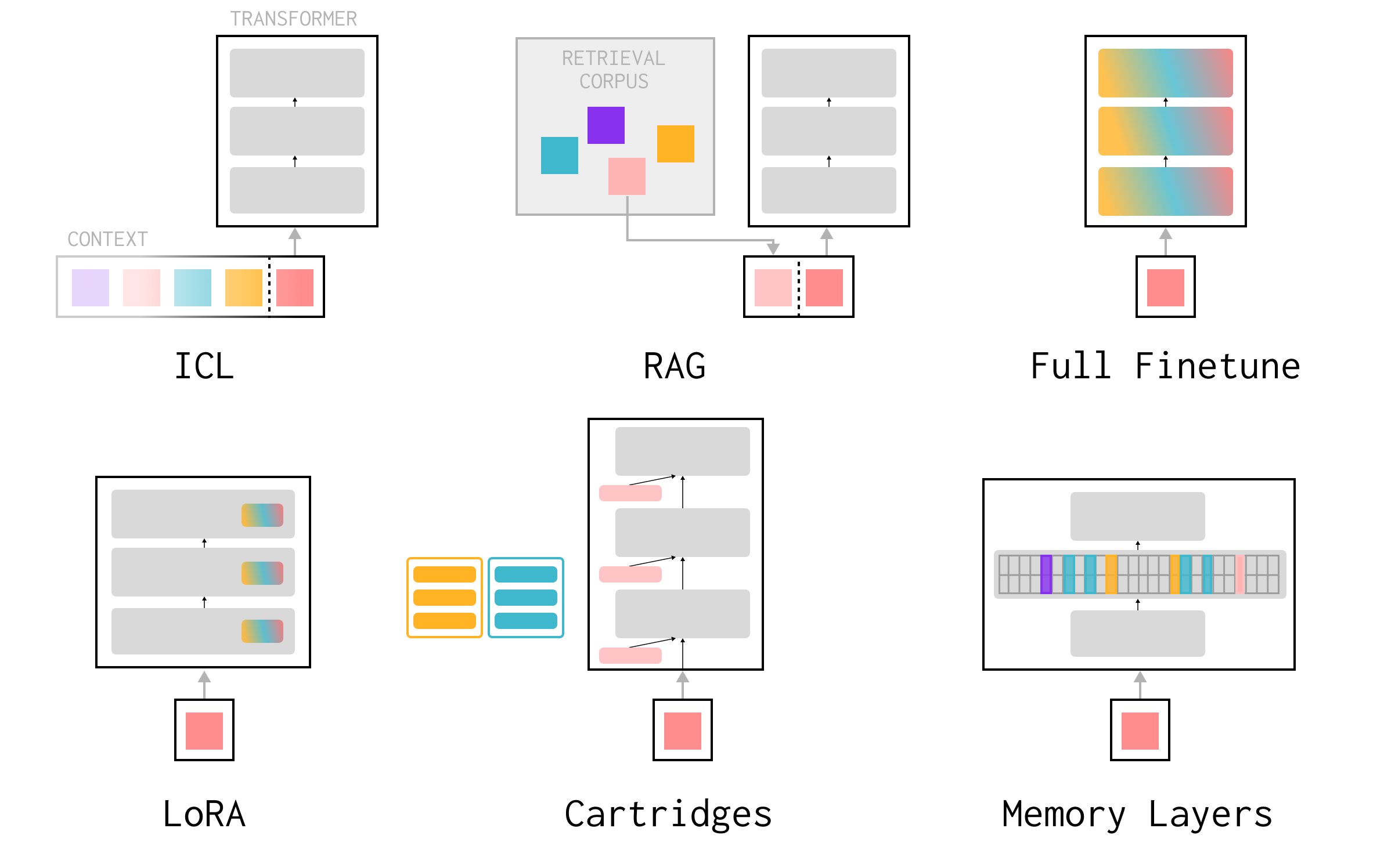
So far, I’ve implicitly assumed a form of continual learning that updates model parameters. Ultimately, we want to make the models themselves smarter over time, in the same way that pretraining does—compressing knowledge from diverse data into weights, rather than building systems around fixed black-box models. However, it’s worth touching briefly on non-parametric methods since they’re the default solution today.

In-context learning (ICL): models get pretty smart in context. I can give the model feedback or put previous interactions in context, and it’s really good at adapting accordingly—up to a point. One problem today is “context rot,” where the model gets confused as the context gets filled with more information, rather than being able to pick out the relevant information as we would expect. Conditioning on previous errors sometimes makes the model more likely to produce errors. This is likely because ICL is inherently limited by the context lengths of the data we’re post-training on. ICL is useful as a ceiling for short-term memory, but without new research it doesn’t yet look like we’ll get infinite context generalization out of the box.

RAG: another approach is to retrieve over a growing buffer of data/experiences, bringing things into context on demand. This is high capacity (just add more documents) and targeted (we don’t need to touch most of the buffer when we add new information), but doesn’t compress knowledge. Consider reasoning and coding tasks. We want the model itself to get better at coding with experience and distill the efforts of its reasoning, not to retrieve previous coding sessions verbatim. Good retrieval is also a bottleneck, particularly for tasks like coding. In a lot of cases, knowing there is a abstractly similar past datapoint to retrieve is half the challenge. Just like humans use both written “scratchpad” memory and internalized memory, I’d expect that future continual learning systems should have both.

A more thorough investigation into non-parametric vs. parametric learning deserves a paper of its own. In our work, we focus on pushing the frontier of parametric continual learning and compare to parametric baselines accordingly.

Finetuning with replay: the simplest parametric baseline is to keep finetuning the full model on new data. This doesn’t lead to targeted updates, but a common solution is to continually replay old data to avoid forgetting. The downside is that replay isn’t a scalable solution to true lifelong learning: imagine rehearsing all the books you’ve ever read every time you code! Additionally, modern models go through multiple rounds of pretraining, midtraining, alignment, etc., making it increasingly complicated to implement this effectively (e.g. we want to mix in pretraining data, but maintain the model’s instruction following capabilities).

Parameter-efficient finetuning (PEFT): LoRA, adapters, prefix tuning, Cartridges: to avoid finetuning all the parameters of the model, we might add a small set of new parameters. By freezing the rest of the model, we get targeted updates, but this is inherently low-capacity. As we grow the amount of experience, we might imagine adding more and more adapters and swapping them out, but it’s unclear when to add new adapters vs. update old ones when the real world doesn’t have discrete “task” boundaries. Ideally, the choice of which adapter or set of parameters to use would also be learnable.

MoEs/modular experts: MoE architectures naturally implement learned routing, and some work has proposed adding new experts to support new domains at test-time. This is high-capacity, learned, and somewhat targeted—depending on the total number of experts, a single expert can still be a large portion of the parameters.

What if we made the experts much smaller and had many more of them? Instead of each of 8-128 experts that each represent broad domains of the data, we might imagine scaling to 1M or 10M tiny (linear) experts, enabling storage and retrieval at a much finer granularity. This way, we get targeted updates through sparsity. This is the key feature of recently-proposed memory architectures: PEER: He et al. 2024, Memory Layers: Berges et al. 2024, UltraMem: Huang et al. 2024.

Memory Layers

I’ll introduce how memory layers work before getting into how our method uses this architecture for continual learning. The idea is simple: a memory layer swaps out one or more of the FFNs in the Transformer with a sparse attention lookup into a pool of learned keys and values.

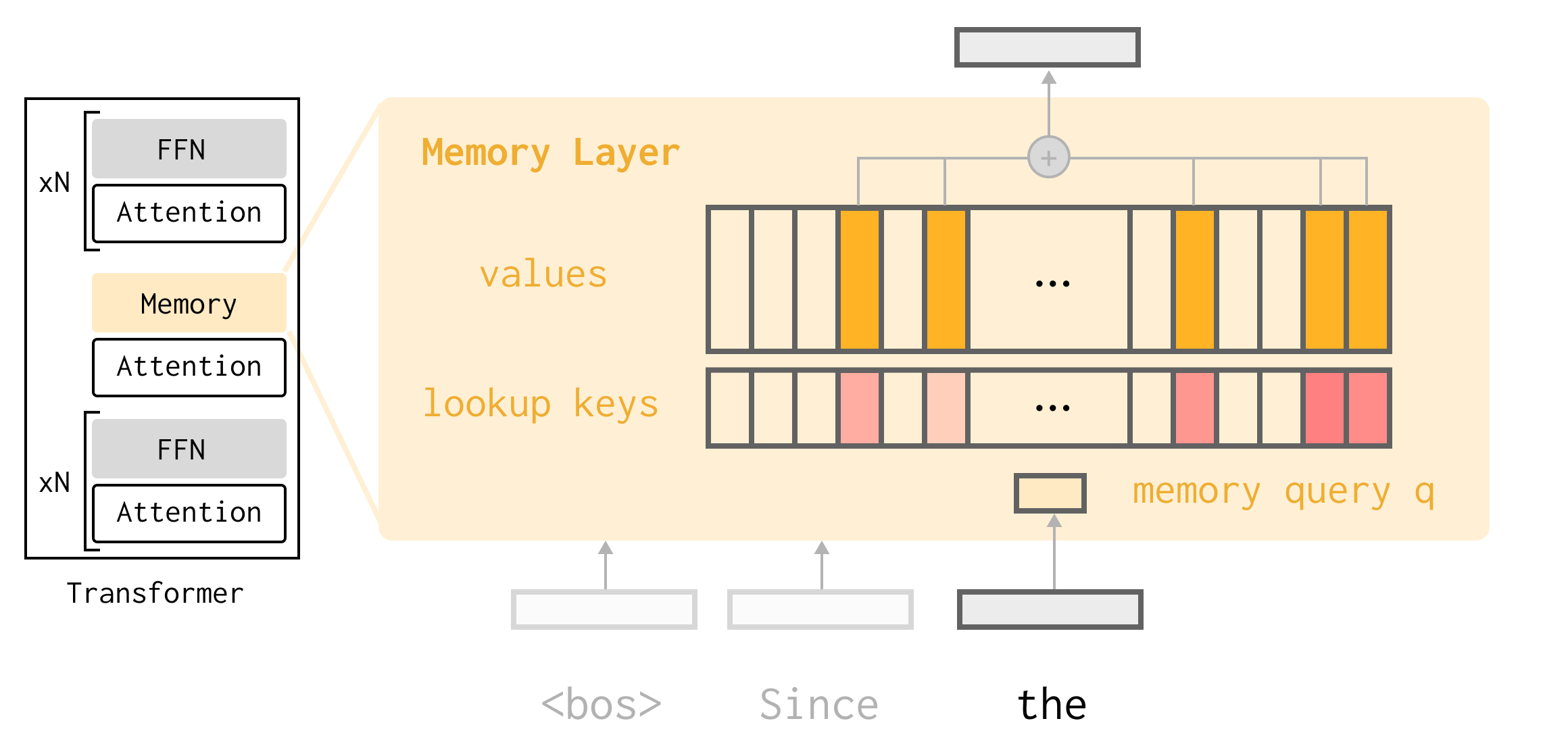
Concretely, the memory pool is a set of \(N\) slots, with learned key and value parameters for each slot \(K \in \mathbb{R}^{N \times d_k}, V \in \mathbb{R}^{N \times d_v}\).

We apply a learned projection to the output of the previous layer \(x\) to get a query \(q(x) \in \mathbb{R}^{d_k}\) and attend into the pool with our favorite operation, dot-product attention. Rather than taking a weighted sum over the entire memory, we only use the top-k most similar slots (where \(K_{\mathbb{I}} \in \mathbb{R}^{k \times d}\) are the top-k keys):

\[\begin{aligned} \mathbb{I} &= \text{TopKIndices}(Kq(x), k) \\ s &= \text{softmax}(K_{\mathbb{I}} q(x)) \\ y &= s V_{\mathbb{I}} \end{aligned}\]

While the memory pool may be on the order of 1M-10M slots, we might only use \(k=32\), a tiny subset of the total parameters (e.g. on the order of 0.03%-0.0002% of total memory parameters).

Finally, we apply an input-dependent gating to get the output of the layer:

\[\begin{aligned} \text{output} &= (y \odot \text{silu}(x^{\intercal} W_1))^{\intercal} W_2 \end{aligned}\]

where \(W_1 \in \mathbb{R}^{n \times d}\) and \(W_2 \in \mathbb{R}^{d \times n}\) are learned projection matrices, and \(\text{silu}(x) = x \,\text{sigmoid}(x)\).

This is the basic idea, along with some additional details like product keys to make the huge lookup efficient. In contrast to attention, the keys and values here are learned parameters, rather than activations. The backward pass nudges the value parameters to be helpful for prediction, and nudges the keys so that the most useful slots are accessed. We might think of the values as “caching” useful information.

Memory architectures have been revisited throughout the years (e.g. Neural Turing Machines from Alex Graves in 2014, or Memory Networks from FAIR in 2015), but only recently have these ideas been scaled up to billion-parameter models and shown to outperform in FLOPs-controlled settings.

We pretrain this architecture on DCLM, enabling the model to learn how to organize its memory pool on a diverse set of data. The exciting thing about memory layers is that the sparsity enables us to do continual learning with minimal forgetting. With memory slots, we have much finer control over what parameters are updated for new data points.

Sparse Memory Finetuning

The main idea of our work is that we can get high capacity, targeted updates with sparsity, enabled by memory layers. The model learns how to organize its knowledge through end-to-end gradient updates, but we can achieve much more selective updates.

Let’s take a look at how memory layer finetuning can enable continual learning on the tasks from our paper. We evaluate parametric continual learning methods on two settings: learning from a stream of facts from TriviaQA, and learning from a stream of documents from Wikipedia from SimpleQA (to simulate reading and retaining information from new documents). In the fact learning setting, we convert TriviaQA questions into statements and paraphrase it to fill a batch, so on each gradient step we want the model to learn one fact.

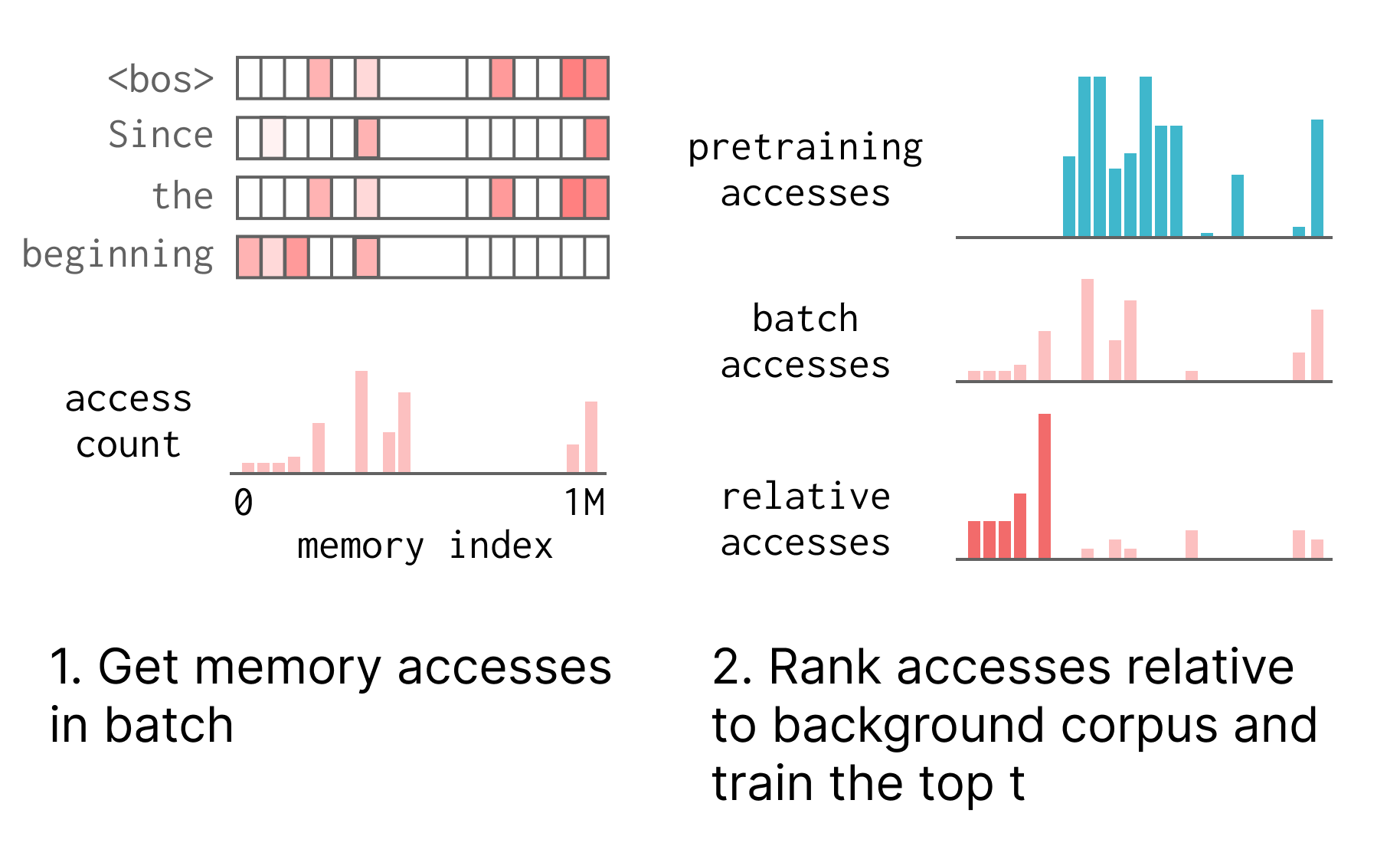
Intuitively, what we’d like to do is only finetune the slots that “store” the fact. For example, given the prefix “Barack Obama was,” the pretrained model might access slots 53, 6111, and 9235 to predict the next token. It’s natural to think of these sparse accesses as storing something meaningful about Barack Obama. However, some of these memory slots might also serve general purposes, such as helping predict syntactic structures or language features (“what word tends to follow was?”).

What we want to do is finetune only the slots that are specific to this data point. This is a common primitive in document retrieval: in TF-IDF or BM25, we retrieve documents where a term in the query frequently appears and doesn’t appear frequently in other documents (discounting the effect of terms like “the” or “and”). We adopt TF-IDF as the ranking metric to count up memory slot accesses: a memory index $i$ ranks highly if it is accessed frequently on this batch and infrequently accessed on other data (we use DCLM pretraining data), suggesting that it is selective to this data sample. We call this sparse memory finetuning.

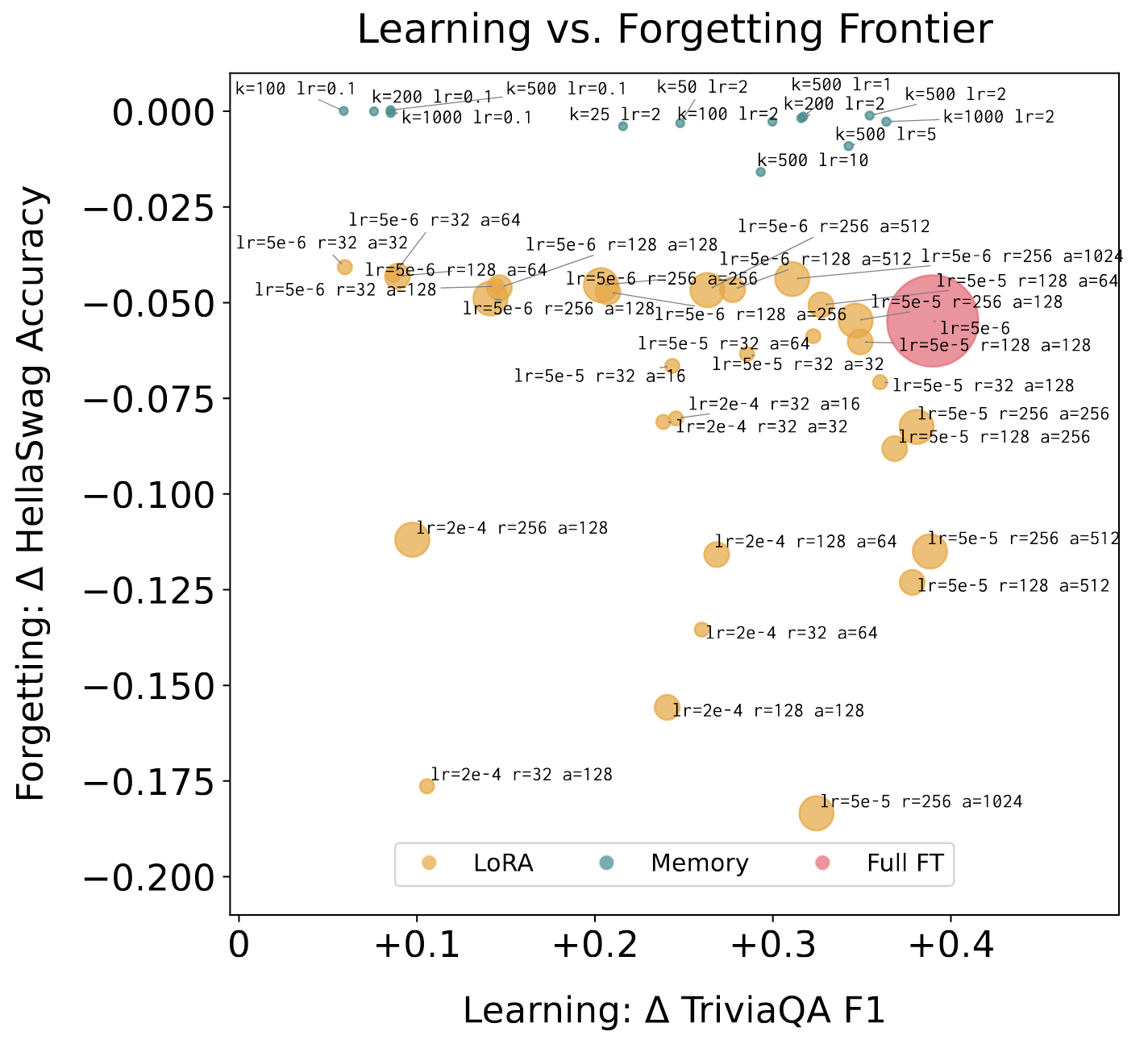
This works really well! We compare to full finetuning and LoRA as baselines, given that LoRA is popularly proposed for continual adaptation/personalization. Both full finetuning and LoRA degrade quite a bit on held-out benchmarks (we use Natural Questions and GSM8K) when learning from new facts. Sparse memory finetuning can learn to the same degree, while exhibiting much less forgetting:

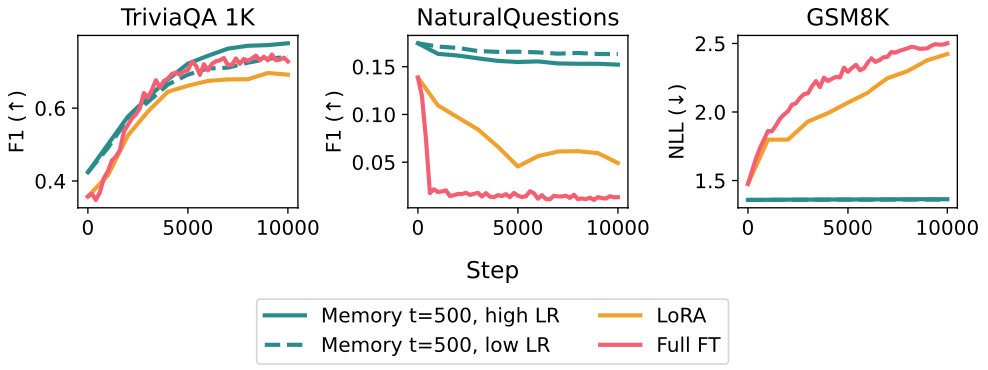
We can better characterize each of these methods by sweeping over the parameters that control learning and forgetting. There is a fundamental tradeoff between the two: to maximize learning, one can specialize the model to a task by updating more parameters at a higher learning rate for more steps; to minimize forgetting, one can (trivially) keep the model fixed at initialization. For full finetuning, the main parameter is learning rate; for LoRA, rank/alpha/learning rate/trainable modules, and for sparse memory finetuning, learning rate/the number of indices we finetune. We can see from this plot that we can increase the learning capacity of memory finetuning without much degradation on held-out tasks.

Looking Forward

I think this paper raises more new questions than answers :) We’ve seen promising results on small models (1.3B base + 1B memory pool) and simple benchmarks. As a next step, it’s important to characterize memory for larger models up to frontier scale (where I’d actually expect memory layers to potentially shine even more, because smaller models are forced into superposition). It’s possible we could go even sparser with larger models + memory pools). And of course, to bridge the gap to real-world continual learning, we really need better benchmarks.

The full paper covers more ablations on finetuning different parts of the memory layer, using different held-out corpora for the TF-IDF reranking, etc., but there are some tidbits worth highlighting:

Optimizer. We initially used AdamW for all methods, and sparse memory finetuning still exhibited much less forgetting than full finetuning and LoRA. However, at some point we realized that the features of the optimizer—adaptive per-parameter step sizes, weight decay, and momentum—can interact with sparsity in unexpected ways. Switching to SGD for sparse memory finetuning led to much less forgetting and could match the performance of AdamW at convergence if we set the learning rates high (lr=2 or 10!). Interestingly, SGD didn’t work as well for full finetuning and LoRA even with a comprehensive sweep, echoing past work that found that Adam isn’t the best choice for continual learning. Various assumptions baked into our favorite optimizers are broken in this setting, and I think it’s worth revisiting some of these design decisions as we move into an “always training” regime.

Interpretability. We did some very basic analysis to investigate to what extent memory slots align with human-interpretable concepts (e.g. storing information about “Barack Obama”). At each token position, we access k=32 memory slots. If we just visualize the ones that are trainable after ranking with TF-IDF, we see that they line up with entity boundaries and “high information content” tokens:

There’s clearly a lot more thorough analysis that could be done here along the lines of memory editing and localization like ROME.

Pretrained vs. post-trained memory. Because memory layers just use attention, there’s a rich design space interpolating between in-context attention or KV cache-based approaches, and memory layers. For example, Cartridges also learn a trainable set of keys and value parameters, but initialize these parameters from scratch to compress a desired corpus and attend over them as part of the context. In contrast, in our work we pretrain the memory layer and attend over the values at an intermediate layer of the network. Switching to a new architecture at pretraining time has a high cost, but there are reasons we might want this (besides the better scaling behavior): the model can learn to organize its memory from scratch, and once we’ve already “allocated” this high-capacity memory pool, there’s a clearer path to learning on multiple tasks and corpora over time. It’s worth exploring the space in between! For example, one could imagine adding a memory pool to a pretrained base model, or slotting in Cartridges to a larger sparse pool over time.

Evaluation. The evaluation setup we used in this paper is clearly just a starting point. We’d expect any continual learning to be able to learn new facts without forgetting other things it knows, how to code, etc. While retrieval is certainly a more natural fit if we only care about continual fact learning, we can think of this as a “table stakes” testbed for any parametric learning method, on the way to more sophisticated continual learning of skills and general kinds of experience (if you’re working on continual learning benchmarks, I’d love to chat!).

My goal in this post was to motivate memory layers as a way to enable continual updates without forgetting, but also to share how I’ve been thinking about the continual learning problem more broadly. Continual learning and memory is a huge, rich space to explore, and at this point in 2025 we’re only just starting to reach the point where we can imagine what it might look like to have models that learn online in the real world—the research is only just beginning.

If you’re working on these problems or exploring applications of models that learn from user feedback, feel free to reach out!